Need Of Complex Numbers

Some quadratic equations which have no solutions in real numbers. 

For Example

1.    

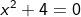
2.   

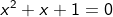
3.   

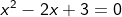
In order to find the solutions of above given or similar quadratic equations, the symbol ” i  ”  was used.  Euler was the first person to introduce the symbol ” i “. where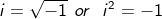          

                    Gauss ( 1777-1855) was a German Mathematician and was a first person to prove  in satisfactory manner that there are some algebraic equations which have real coefficients have complex roots in the form of  .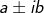

  Note:   complex and irrational roots always occur in pairs.