Let , ) =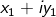
Addition: The sum of two complex numbers is
Subtraction: The difference of two complex numbers is
Multiplication: The product of two complex numbers is
=
Division: The Quotient of two complex Numbers is
=
Remark: A set of complex numbers form a field.