PAKMATH Knowledge Learning Point

Breaking News

Home / Complex Analysis Notes / Polar form of a complex number solutions

Polar form of a complex number solutions

Polar form of a complex number. If z= x + iy is a complex number. Then z = r ( cosθ + sinθ ) is called polar form or trigonometric form of a complex number.

By comparing real and imaginary parts of a complex number, we get

x = r cosθ (1)

y = r sinθ (2)

By squaring above equations and adding we get

$r^2 = x^2 +y^2$

EXAMPLE

Express 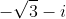$-\sqrt{3} -i$ in polar form.

Solution

With 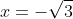$x =-\sqrt{3}$ and y = −1 we obtain

$r = |z| =\sqrt{(\sqrt{-3})^2+ (-1)^2}= 2$

Now

$\frac{y}{x} = \frac{-1}{-\sqrt{3}}=\frac{1}{\sqrt{3}}\$

and

$\theta=tan^{-1}(\frac{y}{x})=\frac{1}{\sqrt{3}}= \frac{\pi}{6}\$

which is an angle whose terminal side is in the first quadrant.But

since the point $(-\sqrt{3}, -1)$ lies in the third quadrant, we take the solution

$tan \theta =\frac{-1}{\sqrt{-3}}=\frac{1}{\sqrt{3}}$

So,

$\theta = arg(z) = \frac{\pi}{6}+ \pi = \frac{7\pi}{6}$

Therefore, polar form of the number is

$z = 2(cos\frac{7\pi}{6} + isin \frac{7\pi}{6})$

Solved Questions of polar form

Polar of $\frac{-34i}{5-3i}$ click here
Polar for of $(-2+2i)(1-i)$ click here
Polar for of $-\sqrt{3}+ i$ click here
Polar for of $-i$ click here
Polar for of $-1-\sqrt{3}i$ click here
Polar for of $-1+i$ click here

CHALLENGE

write the given complex number in polar form first using an argument θ = Arg(z)

1. 2

2. −10

3. −3i

4. 6i

5. 1 + i

6. 5 − 5i

7. $-\sqrt{3}+ i$ click here for solution

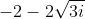
8. $-2 - 2\sqrt{3i}$

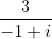
9. $\frac{3}{-1 + i}$

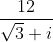
10. $\frac{12}{\sqrt{3} + i}$

Note: If you failed to find any question solution then comments us. We’ll provide you their solutions.

One comment

Ahmed malik
31/03/2021 at 7:41 AM

Plz provide the solution

Reply

Leave a Reply Cancel reply