Polar form of a complex number
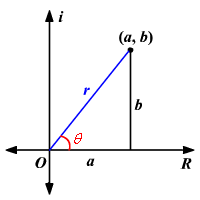
The polar coordinates of a P are (r,θ) where r is known as modulus and
θ is the argument of a complex number Z.
From above figure
a = r cosθ
b = r sinθ
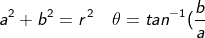)
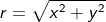
or
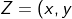=x+iy=&space;r(cos&space;\theta&space;+&space;i&space;sin&space;\theta&space;))
The plane is known as Argand plane or Argand Diagram or complex plane or Gaussian plane.