Locus of complex number play a very important role in the complex analysis. Today we learn how to represent and find the locus of a complex number. We can also prepare Multiple choice questions about this topic and complex analysis.
Let P(Z) be the property that satisfied by a complex number z = x + iy.
Let there is a complex number that may satisfy the condition |z| =2. Then the set A = { z : |z| = 2 }
⇒ { ( x, y} : | z | =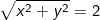 
}
⇒ { ( x, y} : | z | =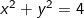 
}
is called the locus of the complex number z satisfying | z | =2.
From above the locus of complex number z represents a circle with the center at ( 0, 0 ) and radius r = 2.
EXAMPLE: Find the locus of a complex number z = x + iy, such that for a fixed point, |z-z1 |= a
Solution:
As A = { z ; |z-z1 | =a }
⇒ { ( x, y} : | &space;+&space;i&space;(y-y_1))
| = a }
⇒ { ( x, y} : &space;^2+&space;i&space;(y-y_1)^2&space;=&space;a^2)
}
which is a circle with center at )
and radius r = a
EXAMPLE: Let
Solution:
We know that +&space;i&space;(y-y_1))
.
First we find the argument of z
so
⇒
Because Arg(z-z1) =
So =
And = 1
So, x-x1= y-y1 or x – y = x1-y1