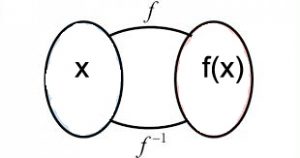
In this post we define inverse function and also provide an example to clear the concept of it.
The inverse function of f denoted by f-1 is a function from Y onto X and is defined by x= f–1(y) for all x in y if and only if as y=f(x) , for all x
The set X of all possible input values is known as domain and the set of all values of f(x) as x varies through X is called range of a function.
Example: Let f : R → R be the function defined as f(x)= 2x+1 then find f -1(x)
Solution.
As f(x) = 2x+1
y – 1 = 2 x
→ (1)
we know that f( x ) = y
x = f -1(y)
By putting value of x in (1) we get
By Replacing y = x we get

For other Definitions Click here